Mutual Exclusion

For mutual Exclusion in Distributed System, we need to guarantee 3 propterties:

1. Safety (essential): Nothing bad happens
2. Liveness (essential): Every request is granted eventually
3. Ordering (desirable): Requests are in order of they made

Common solution such as semaphore is not plausible in DS since there is not shared resources in DS.

So, we have different solution for this problem:

Central Algorithm

1. Elect a leader using election algorithm.

2. Construct Queue for request, when one is allowed to access resource(critical section), give it a token. When it is finished, give the token back to master.

   For this algorithm, safety and eventual liveness is guaranteed, FIFO ordering is guaranteed in order of requests received at master. The bottleneck of it is the master server.

Ring-based Mutual Exclusion

N processes organized as ring, exactly token is passed around the ring.

1. If one wants to enter the critical section, wait for the token.

2. When receive a token and is in critical section, use it then pass to the successor.

3. If not in critical section, directly pass to the successor.

For this algorithm, we can see that the best case and worst case is largely different since it is based on where the token is and when a process enters a critical section.

Ricart-Agrawala’s Algorithm

Each process has its own “state” indicating its status, including: “Wanted”, “Held”, “Released”.

When one process $P_i$ wants to enter critical section, it:

1. For $P_i$, set state = “wanted”, then multicast “Request” in form of <$T_i, P_i$> to all processes, where $T_i$ is lamport timestamp, $P_i$ is process id used to break tie.
2. wait until all processes send back “Reply” message, then change state = “Held” to enter the critical section
3. For those who received <$T_i, P_i$>, if its state = “Held” or it is also in “wanted” and its timestamp is smaller/earlier than the request, it put the request into local queue. Else, it send “Reply” back to $P_i$ .

When one process $P_i$ wants to exit critical section, it changes state to “Released” and send “Reply” to all queued requests.

Example:

Current no other request:

N32 sends request

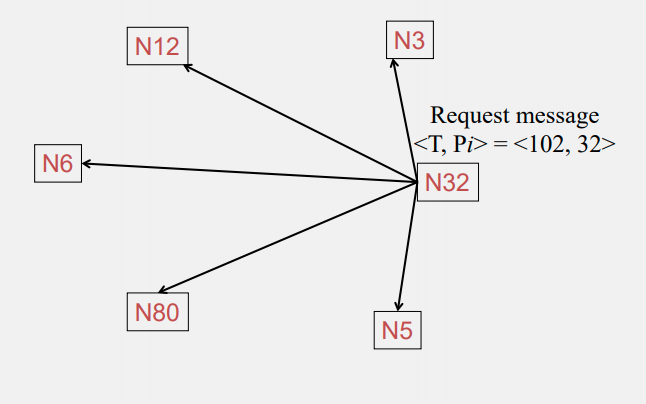
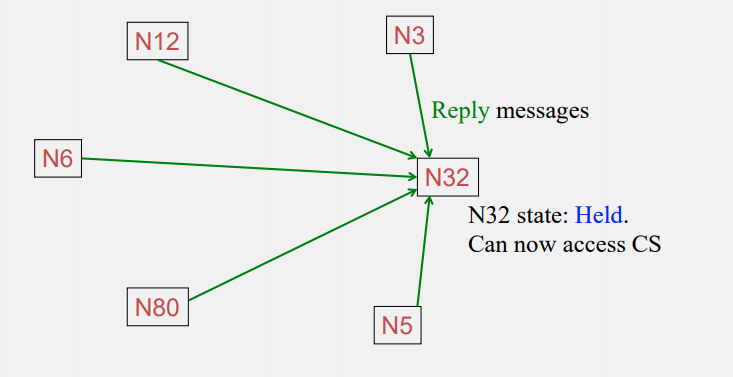
All other replys

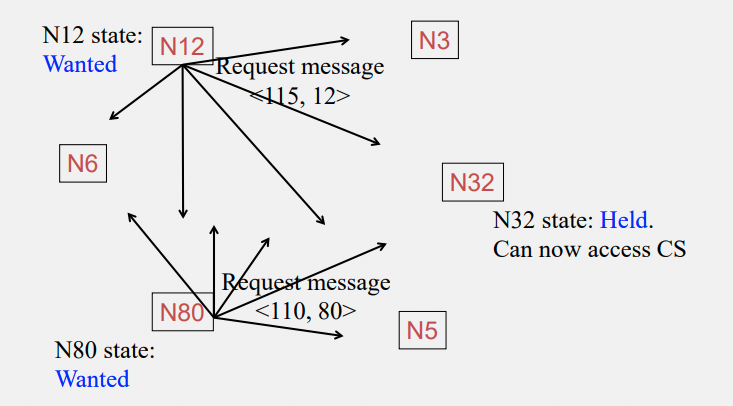
Concurrent requests occur: N12 and N80 wanted to access

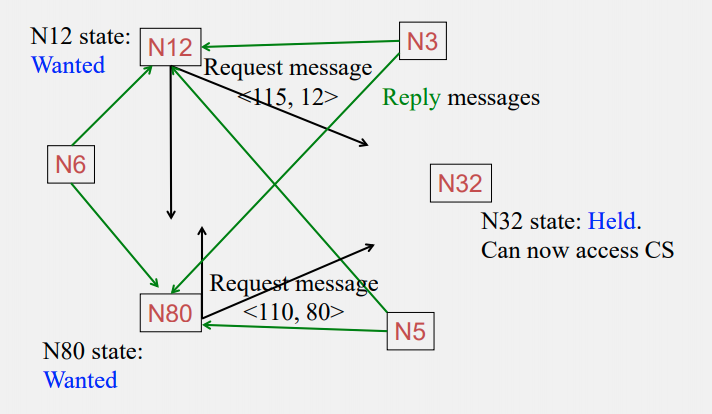
Enqueue the requests, wait for N32 to finish access

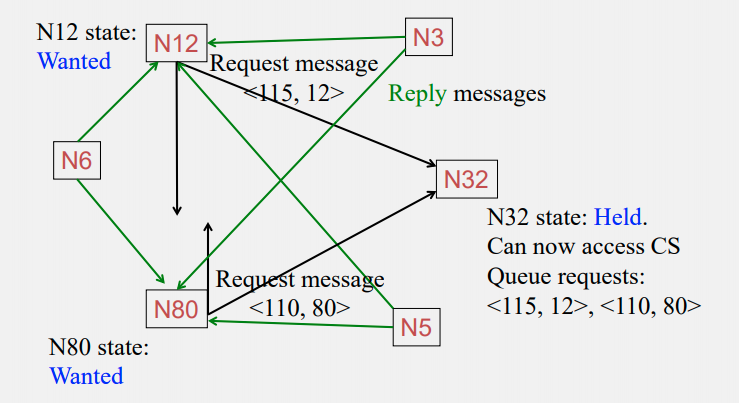
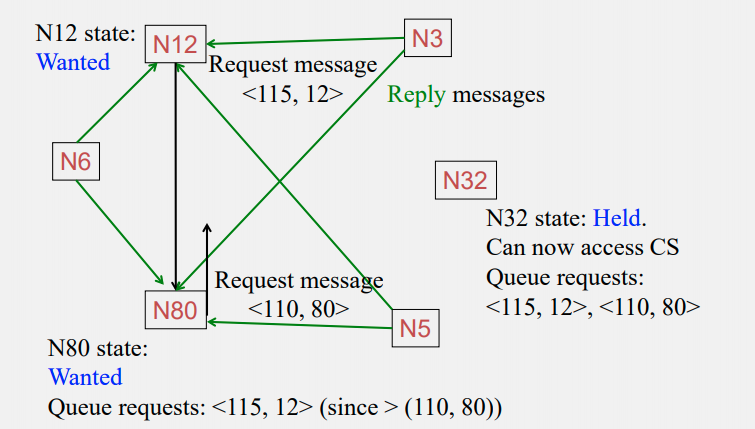
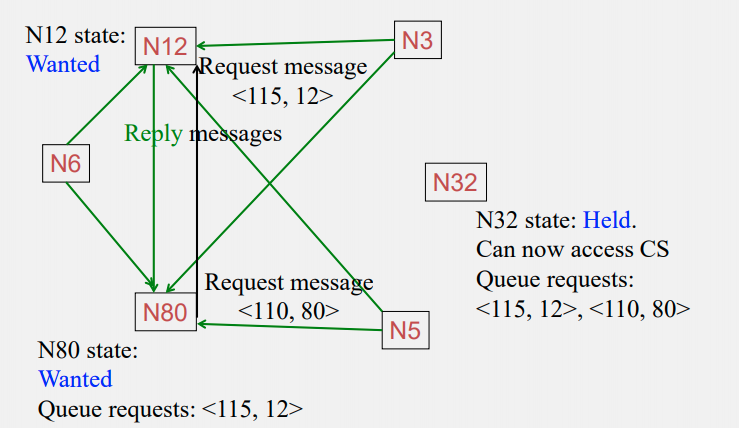
N32 finish, N80 starts access

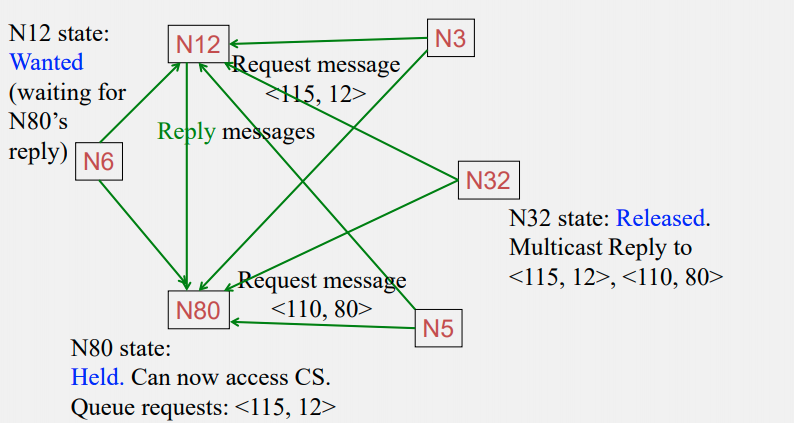
For this algorithm, Safety and liveness is guaranteed, ordering is guaranteed in the order of lamport timestamp, and the worst case is for a process $P_i$ to wait for N - 1 processes to send Reply back.

Maekawa’s Algorithm

Each process is in a voting set, and each process belongs to its own voting set.

The intersection of any two voting sets must be non-empty, kinda like quorums.

In terms of size, each process belongs to M other sets, each sets is of size K, and K = M = $\sqrt{N}$ is proved to be best.

One approach is to put N processes into $\sqrt{N}$ * $\sqrt{N}$ matrix, for each process p, v = i + j, where i is row number of p and j is column number.

Compared to Ricart-Agrawala’s Algorithm, it only requires processes in group to send reply (vote) back. Each process maintains a local variable called “votes”.

Pseudocode as follows:

state = Released, voted = false

enter() at process Pi:
	state = wanted;
	muticast Request message to all processes in Vi
	Wait for Reply (vote) messages from all processes in Vi (including self)
	state = Held
	
exit() at process Pi:
	state = Released
	Multicast Release to all processes in Vi
	
When Pi receives a Request from Pj:

 	if (state == Held or voted ==  true):
 		enqueue Request
 	else:
 		send Reply to Pj and voted = true
 
When Pi receives a Release from Pj:
	
	if (queue is empty):
   		voted = false
    else : 
    	dequeu head of queue, Pk
    	send Reply only to Pk
    	voted = true

• 本文作者： Yu Wan
• 本文链接： https://cyanh1ll.github.io/2021/01/14/mutual/
• 版权声明： CYANH1LL